混合布尔算术MBA

(全文太单调了，用banana搞一张图😁

定义与应用

定义

混合布尔算术表达式（Mixed Boolean-Arithmetic Expression, MBA）是一种形式化表达式，其语义结合了布尔逻辑运算与整数（或更一般地，环/域上的）算术运算，并通过控制流结构（如条件表达式）或代数恒等式将二者交织在一起。其形式化定义如下：

设$\mathbb{B} = \{0, 1\}$ 为布尔域，$\mathbb{Z}$（或$\mathbb{Z}_n$，其中$n = 2^w$ 对某字长$w \in \mathbb{N}^+$）为整数（或模$n$ 整数）算术环，令$\mathcal{V}$ 为有限变量集合。一个混合布尔算术表达式 是由以下语法归纳定义的表达式$E$：

$$ \begin{aligned} E &::= c \mid x \mid E_1 + E_2 \mid E_1 - E_2 \mid E_1 \cdot E_2 \mid \ldots \quad &\text{(算术部分)} \\ &\quad \mid \neg B \mid B_1 \land B_2 \mid B_1 \lor B_2 \mid B_1 \oplus B_2 \quad &\text{(布尔逻辑部分)} \\ &\quad \mid \texttt{ite}(B, E_1, E_2) \quad &\text{(条件表达式)} \\ B &::= (E_1 \,\diamond\, E_2) \mid b \mid \neg B \mid B_1 \land B_2 \mid \ldots \quad &\text{(布尔谓词)} \\ \end{aligned} $$

其中：

$c \in \mathbb{Z}$ 为整数常量，$b \in \mathbb{B}$ 为布尔常量；
$x \in \mathcal{V}$ 为变量，其类型可为整数或布尔（或统一视为整数，布尔值以 0/1 表示）；
“$+, -, \cdot$” 等为$\mathbb{Z}$（或$\mathbb{Z}_n$）上的标准算术运算；
“$\neg, \land, \lor, \oplus$” 为$\mathbb{B}$ 上的布尔运算；
“$\diamond \in \{=, \neq, <, \leq, >, \geq\}$” 为关系谓词，生成布尔值；
$\texttt{ite}(B, E_1, E_2)$ 表示“if-then-else”：当布尔条件$B$ 为真时取$E_1$，否则取$E_2$；
所有子表达式均可嵌套，允许布尔表达式出现在算术上下文中（通过将布尔值解释为 0/1），反之亦然。

事实上，我们实际要处理的不会有关系谓词和条件语句，即要处理的是由加减乘和与或非异或组成的表达式，形式化有点抽象，下面给出一个经典的例子：

$$ x + y = (x \oplus y) + 2 \cdot (x \land y) $$

对于任意两个整数$x, y$该表达式成立，左侧为简化的算术代数，右侧为布尔代数与算术代数结合的复杂形式，在固定字长(如32位/64位)下等式横成立，即在环$\mathbb{Z}_{2^w}$中两者是可以转换的，此处可从两个角度理解：

1.$x \oplus y$为不带进位的加法，$x \land y$为加法的进位，$2 \cdot$即进位左移$ <<1$，所以等价于$x + y$

2.另外还有中理解，直接用集合论，可以画个维恩图，$x \oplus y$即为集合不相交的部分，$x \land y$为集合交集，交集需要乘2

附：可以在这个网站体验一下～

化简挑战

首先说简化，它是对人类理解而言的，其实没有精准定义，Eyrolles ⁵给出了基本想法：

减少表达式的大小应该使其更容易理解和操作。

减少(MBA aspect)，即表达式中混合两种运算符的部分，应该允许我们有更大的部分只包含一种类型的运算符。然后，我们可以使用现有的方法来简化纯算术或位表达式。

有了此目的再看怎么做，正向的看计算机本身支持这两种基本计算，它使用$n$ 位二进制补码整数进行加、减、乘、移位和比较等算术运算，这些操作会映射到模环 $Z/(2^n)$，而位运算（如异或 $\oplus$、或 $\vee$、与 $\wedge$、非 $\neg$）是在布尔代数 $(B_n, \wedge, \vee, \neg)$ 上操作，所以MBA运行没有任何问题，而且单看每类操作都有成熟的化简方法，但是将它们结合起来后，就涉及多个数学域，现在是没有通行的简化算法的(可类比大整数分解)，当然³给出了复杂度说明，它在最坏情况下是 NP-hard 问题，具体来说，他们指出与 MBA 相关的识别问题属于 NP-complete 类别：

BA[n]-sat： 对于给定的多项式 MBA 函数 $f$，找到输入值 $a_1, \ldots, a_m$ 使 $f \neq 0$。
BA[n]-recog： 对于多项式 MBA 函数 $f$ 和 $g$，找到输入值 $a_1, \ldots, a_m$ 使 $f \neq g$。

因为它们可以很容易地从布尔 SAT 问题的 NP-complete 属性中推导出来，如果不具备高效的简化器，要识别混淆代码的功能性，将面临巨大的 $BA[n]$-recog 函数识别负担。

还好，尽管理论上很难，但针对具体情况还是存在一些攻击手段，后文会详细分析。

用途

MBA可用于逻辑混淆和常量混淆，典型的使用场景如，Blazytko和Altamura在Recon25上展示了多种示例¹：

1.不透明谓词：用MBA构造永真/永假条件，可添加虚假控制流或垃圾指令等

uint8_t opaque_predicate(uint8_t x, uint8_t y) {
    // 此处 k1 k2 恒等
    uint8_t k1 = 96 + 159 * (y ^ x) + 160 * y + 194 * (y | x) + 96 * ~x;
    uint8_t k2 = 193 + 64 * ~y + 65 * (y & y) + 130 * x + 129 * ~x;
    if (k1 != k2) {
    // dead code
        return x - y;
    }
    return x + y;
}

2.逻辑混淆：将程序中原本简单、可识别的运算，全部替换成它们等价的、复杂的 MBA 表达式

// 2 * x - y
uint8_t hidden_computation(uint8_t x, uint8_t y){
    int k1 = (x & (((x & y) + (x & y)) + (x ^ y)));
    int k2 = ((x ^ y) + (x & y) << 1) - y;
    int k3 = (x ^ (((x & y) + (x & y)) + (x ^ y)));
    return k1 + k2 + k3;
}

3.常量混淆：用MBA将常量隐藏起来

// 42
uint8_t constant(uint8_t x, uint8_t y) { // 这里的x y是引入的干扰变量，实际值不会影响计算结果
    uint8_t k1 = 202 + 231 * (y | x) + 244 * (x | y) + 7 * (y & y);
    uint8_t k2 = 180 * y + 85 * (y ^ y);
    uint8_t k3 = 155 * (x | x) + 139 * (x ^ x) + 206 * (x & y);
    uint8_t k4 = 174 * (y | y) + 65 * (x & x);
    uint8_t k5 = 115 * x + 67 * ~x + 93 * ~y;
    uint8_t k6 = 35 * (y ^ x) + 246 * (x ^ y) + 63 * (y & x);
    return k1 + k2 + k3 + k4 + k5 + k6;
}

4.白盒密码：就是常量混淆和逻辑混淆的结合体

构造

MBA 表达式的构造或转换通常通过迭代应用以下两种变换来实现混淆：

表达式匹配与重写 (Expressions Matching and Rewriting):
- 选取原始表达式中的一部分 $p$，并使用已知的一系列重写规则或 MBA 恒等式将其替换为语义等价但更复杂的表达式。
- 例如，加法 $x+y$ 可以被重写为等价的表达式 $(x \lor y) + (x \land y)$。其他示例恒等式包括：
  - $x+y \to (x \lor y) + y - (\lnot x \land y)$。
  - $x \oplus y \to (x \lor y) + y - (\lnot x \land y)$。
- 通过这种方法，可以不断地将操作符（如加法、减法、乘法等）转化为具有多个项的高阶多项式 MBA 表达式。
恒等式插入 (Insertion of Identities) / 功能组合 (Functional Compositions):
- 给定一个可逆函数 $f$，表达式的任何部分 $p$ 都可以被替换为等价的表达式 $f^{-1}(f(p))$。
- 当处理一个函数 $f$ 时，可以将其重写为 $S^{-1} \circ (S \circ f \circ T) \circ T^{-1}$ 的形式，其中 $S$ 和 $T$ 是可逆函数。随后，可以通过对中间表达式 $(S \circ f \circ T)$ 应用第一种方法（恒等替换），再进行组合，从而得到一个新的 $f$ 表达式。

基于匹配与重写

这个非常直观，它的关键是一张重写规则表，表里有大量表达式的等价形式，通过递归的匹配病替换等价表达式来实现MBA表达式构造，如Loki¹⁰有84700个匹配重写规则，通过多次递归应用就能取得极强的混淆效果：

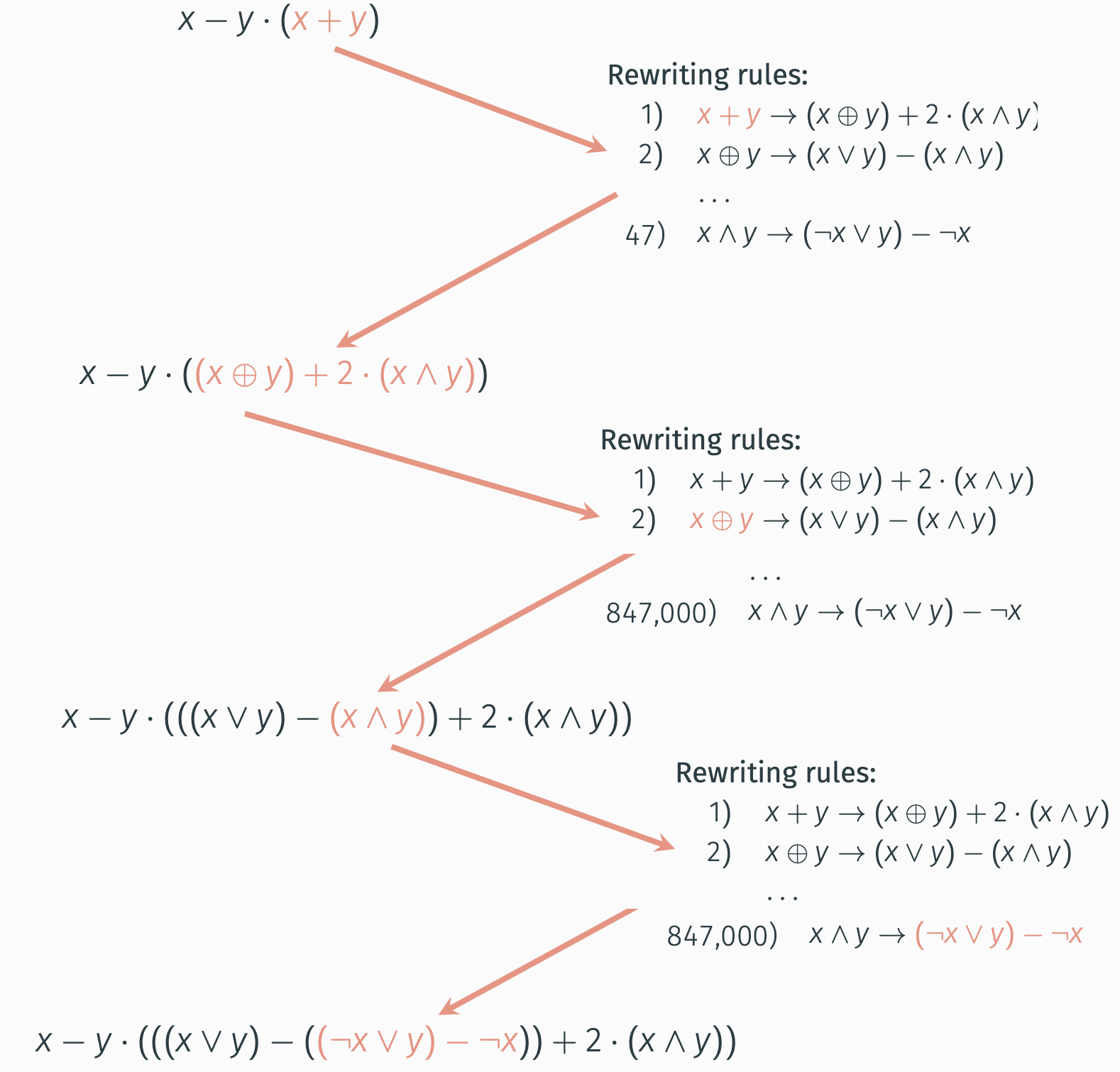
基于零函数和置换多项式的构造

MBA 混淆的经典应用是隐藏软件中的常量 $K$。这种构造方式结合了可逆多项式和零函数：

选择可逆置换多项式：置换多项式$P(x)$ 和它的逆 $Q(x) = P^{-1}(x)$，这两个函数都定义在 $Z/(2^n)$ 环上。
构造零函数：选择一个线性 MBA 恒等式 $E$ 或一个零函数 $h(x)$，使其在 $BA[n]$ 代数中恒等于零，即 $E=0$。
结合生成混淆表达式：原始常量 $K$ 可以表示为 $K = Q(P(K))$，此时依然能轻松化简，所以还需要再通过将零函数 $E$ 插入到内部表达式中，构造混淆表达式：$K = Q(E + P(K))$，展开 $Q(E + P(K))$ 得到一个包含多个变量、多项式形式的 MBA 表达式，其输出值仍是 $K$，但难以化简

现在开始看怎么找可逆置换多项式和零函数

置换多项式构造

Rivest(RSA的R)研究了模 $2^w$ 意义下的整数环 $\mathbb{Z}_{2^w}$ 上的置换多项式（Permutation Polynomials），即那些诱导出 $\mathbb{Z}_{2^w} \to \mathbb{Z}_{2^w}$ 上双射的多项式函数⁴ 。Rivest 给出了一个简洁且实用的充要条件，用于判断一个整系数多项式：

$$ P(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_d x^d \in \mathbb{Z}[x] $$

在模 $2^w$（$w \geq 2$）下是否为置换多项式。多项式 $P(x)$ 在 $\mathbb{Z}_{2^w}$ 上是置换多项式当且仅当以下三个条件同时成立：

线性系数 $a_1$ 是奇数（即 $a_1 \equiv 1 \pmod{2}$，它保证了函数的线性独立性，确保 $P(0) \not\equiv P(m) \pmod n$
偶次项之和$(a_2 + a_4 + a_6 + \dots)$ 是偶数，它确保多项式在最基础的二进制层面（模 2）仍然是一个置换
大于1的奇次项之和$(a_3 + a_5 + a_7 + \dots)$ 是偶数，它确保从模 $2^{w-1}$ 提升到模 $2^w$ 时，奇数输入的映射满足 $P(x+m) \equiv P(x)+m$

注意：常数项 $a_0$ 可以是任意整数（不影响置换性，只影响平移）

初代目

Rivest给出了判别方式，但怎么求这类多项式的逆是个问题，首先是Zhou等人³提出的一类特殊的置换多项式，即满足$a_1$ 是奇数且剩余项全是偶数，这个特殊的子集特别便于计算逆多项式，原文给出了计算方法，逆多项式和原式结构一样，需计算逆多项式 $g(x)$ 的系数 $b_j$ ，首先需要定义递归项 $\mathbf{A_k}$（其中 $2 \le k \le m$）：

$$ \mathbf{A_m = -a_1^{-m} a_m} \text{ (这是最高项，非递归) } $$

$$ \mathbf{A_k = -a_1^{-k} a_k - \sum_{j=k+1}^m \binom{j}{k} a_0^{j-k} A_j} \quad \text{(对于 } \mathbf{2 \le k < m} \text{)} $$

于是就可以计算了：

最高次项系数 ${b_m}$： ${b_m = -a_1^{-m-1} a_m}$
中间高次项系数 ${b_k}$ (其中 ${m-1 \ge k \ge 2}$，依赖于 ${A_j}$ 和 ${b_1}$ 的中间结果)： ${b_k = -a_1^{-k-1} a_k - a_1^{-1} \sum_{j=k+1}^m \binom{j}{k} a_0^{j-k} A_j}$
一次项系数 ${b_1}$： ${b_1 = a_1^{-1} - a_1^{-1} \sum_{j=2}^m j a_0^{j-1} A_j}$
常数项系数 ${b_0}$： ${b_0 = - \sum_{j=1}^m a_0^j b_j}$

例如，对于三次多项式 ${f(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0}$ 属于 ${P_3(\mathbb{Z}/(2^n))}$，其逆多项式 $f^{-1}(x)$ 的系数也有一个显式的展开式：

$$ f^{-1}(x) = (-a_1^{-4} a_3)x^3 + (-a_2 a_1^{-3} + 3 a_0 a_1^{-4} a_3)x^2 + (a_1^{-1} + 2 a_0 a_1^{-3} a_2 - 3 a_0^2 a_1^{-4} a_3)x - a_0 a_1^{-1} - a_0^2 a_1^{-3} a_2 + a_0^3 a_1^{-4} a_3 $$

满足这种条件的多项式有无数个，即变化多端，可以防止被轻易识别！

进化版

Barthelemy等人²研究了任意Rivest所提的二元置换多项式的求逆算法，他们探索了两种算法，最终选择了更高效的牛顿法变种，这里只说该方式，原始牛顿法是求函数根/解决最优化问题的，这里被改成了求函数组合逆，即寻找 $g$ 使得 $f \circ g = X$（其中 $X$ 是恒等函数 $x \mapsto x$），迭代公式为：

$$ g_{i+1} = g_i - g_i' \times (f \circ (g_i - X)) $$

要用牛顿法需要满足两个条件：

1.$f(0) = 0$，显然若$a_0 \neq 0$则不成立，不过$a_0$不影响置换，它只是移位，所以可以先去掉它，算完了再恢复(-$a_0$)

2.$f'(0)$ 是可逆的，由Rivest的定义，$a_1$是奇数，所以它在$Z_{2^n}$ 中一定是可逆的

但额外的，$Z_{2^n}$ 又引入了新的挑战，恒等函数 $X$ 对应的多项式并非是唯一的：

$$ g(f(x)) = x \mod 2^n \quad \not\Leftrightarrow \quad g \circ f = X $$

这会导致迭代无法收敛，作者提出在规约多项式环 $F(Z_{2^n})$ 上使用牛顿法，规约多项式环 $F(Z_{2^n})$ 是在零理想 $I$ 上的商群 $Z_{2^n}[X]/I$ 的子群，即每次迭代后都会讲结果模零理想(后文介绍计算方法)到最简形式再进行下一轮迭代，此方法整体复杂度大约为$O(d_n^2 \times \sqrt{n})$。

零函数与零理想

零函数恒等式

Zhou等人提出如下方式：首先，定义一个 $t$ 个变量 $x_1, \dots, x_t$ 上的线性 MBA 表达式 $e$：

$$ \mathbf{e = \sum_{j=0}^{s-1} a_j e_j} $$

其中：

$x_i$ 是 $n$ 位字 $B^n$ 上的变量。
$e_j$ 是基于 $x_1, \dots, x_t$ 的位运算表达式（bitwise expressions）。
$a_j$ 是 $\mathbb{Z}/(2^n)$ 上的整数常数（系数）。

然后构建真值表矩阵 $\mathbf{A}$，为了确定 $e$ 何时等于 $0$，需要将每个位运算表达式 $e_j$ 转化为其对应的布尔函数 $f_j$：

对于每个 $j \in {0, \dots, s-1}$，计算布尔表达式 $f_j$ 的真值表。由于有 $t$ 个变量，真值表有 $2^t$ 行。
将 $f_j$ 的真值表（即 $2^t$ 个输出值）写成一个列向量 $\mathbf{V}*j = (v*{0,j}, v_{1,j}, \dots, v_{2^t-1, j})^T$。

构建 $2^t \times s$ 的 ${0, 1}$-矩阵 $\mathbf{A}$，其中 $\mathbf{V}_j$ 是矩阵的第 $j$ 列：

$$ \mathbf{A} = (\mathbf{V}_0 \mid \mathbf{V}*1 \mid \dots \mid \mathbf{V}*{s-1}) $$

矩阵 $\mathbf{A}$ 中的元素 $v_{i, j}$ 是 $\mathbb{Z}/(2^n)$ 上的 ${0, 1}$ 值。此时表达式 $e$ 成为恒等式 $\mathbf{e = 0}$（即无论输入 $x_1, \dots, x_t$ 取何值，输出都为 0）的充要条件是线性系统 $\mathbf{A} \mathbf{Y} = \mathbf{0}$ 在环 $\mathbb{Z}/(2^n)$ 上存在解 $\mathbf{Y}$，$\mathbf{Y}$ 即待确定的系数向量：

$$\mathbf{Y}*{s \times 1} = (a_0, a_1, \dots, a*{s-1})^T$$

如果矩阵 $\mathbf{A}$ 的列向量在 $\mathbb{Z}/(2^n)$ 上线性相关，则该线性系统 $\mathbf{A} \mathbf{Y} = \mathbf{0}$ 必然存在非零解 $\mathbf{Y}$。这个非零解 $\mathbf{Y}$ 提供了系数 $a_j$，从而构造了一个非平凡的线性 MBA 恒等式。现在就是要让它线性相关，有两种方法能保证：

增加表达式数量 $s$： 当选择的布尔表达式 $e_j$ 的数量 $s$ 大于变量所有输入组合的数量 $2^t$ 时，列向量集合必是线性相关的。例如，对于 $t=2$ 个变量 $x, y$，有 $2^2=4$ 种组合。如果选择了 $s \ge 5$ 个布尔表达式，它们必然是线性相关的
利用已知相关性： 选择一组已知具有代数恒等关系的布尔表达式。例如，对于 $t=2$ 个变量 $x, y$，Zhou 等人给出的一个恒等式使用了 $s=5$ 个表达式 $\{x, y, x \lor y, \neg(x \land y), 1\}$。这五个真值表向量在 $Z/(2^n)$ 上是线性相关的，从而导出了恒等式 $x + y - (x \lor y) + (\neg(x \land y)) - 1 = 0$

这里面还有个关键点，MBA 表达式和恒等式是基于 $BA[n]$ 定义的，这个 $n$ 可以是任意正整数，所以此处可以用1比特来做运算，而运算的结果是可以扩展到任意比特的！

零理想

Barthelemy等人的论文中，生成集$\{P_0, \dots, P_{i_{max}}\}$是通过考虑所有可能的根（包括奇数和偶数）来定义的。对于$i$从$0$开始递增直到$i_{max}$，多项式$P_i$的形式如下：

$$P_i = 2^{n-i-t_i} \prod_{j=0}^{2^i-1} (x-j) \quad$$

其中：

$n$是位数（例如，对于 32 位整数，$n=32$）
$t_i$是满足$2^l$整除$i!$的最大整数$l$。（它其实是$i!$里的素因子2的个数）
$\prod_{j=0}^{2^i-1} (x-j)$是一个乘积项，它包含了$Z/(2^n)$上的$2^i$个连续整数根。

这里简单说下推导过程，先看乘积项$T_i = \prod_{j=0}^{2^i-1} (x-j)$，它是$2^i$个连续整数的乘积，它可以被$2^i i!$整除(这其实有问题，该结论只针对连续偶数的乘积，但用着没错，作者其实用的$Z/(2^n)$上的可逆元素$Z_{2^n}^*$上的零理想$I^*$来推导的)，又因为$2^l$能整除$i!$，所以它可以被$2^{i+t_i}$整除；再结合系数项有$2^{n-i-t_i} \times 2^{i+t_i} = 2^n$，即$P_i$一定是$2^n$的倍数，那么它在模$2^n$下恒等于$0$。

除了上面提到的多项式化简，零函数还可用于生成不透明零来混淆常量（如$K = f^{-1}(h(x) + f(K))$），或混淆算术表达式$g(x)$（如将其重写为$(h(x) + 1) \times g(x)$ 并展开）

攻击

基于规则匹配

这是最直观的，对于简单的基于匹配重写的表达式，如果我们有全部的重写规则，则可以反过来通过匹配恢复它们，Eyrolles最初在⁵描述的就是该方法，后来他们提出了SSPAM¹²，它支持逆匹配重写，它内置了zhou等人以及后续研究遇到的多种变换规则，且可以自定义新规则，同时它还支持一些简单算术的识别与计算，但这里面最需要关注的还是匹配方法，它提出的也是之后几乎所有其它方法涉及匹配时都会用到的，将表达式转换为AST，在表达式树里做匹配，在匹配时对于存在交换律的操作它会同时处理两种顺序。

匹配除了受固定模式的限制外，规约的顺序也会影响规约的结果，fvrmatteo等人提出了等式饱和¹³的思路(这篇文章主要优化的是下文要提的基于合成的方法，但主要工作是在匹配过程的优化上)。

基于位爆炸(Bit-blasting)

梦回计组，在计算机中算术运算是由逻辑运算完成的(在ALU)，以加法为例，它实现为一个全加器，即将 $n$ 比特变量 $X$ 和 $Y$ 的加法 $R = \text{add}(X, Y)$ 转化为其各个比特的布尔运算，全加器通过计算输入位 $x_i$、 $y_i$ 以及来自低位的进位 $c_i$ 来确定结果位 $R_i$ 和向高位的进位 $c_{i+1}$，对于结果 $R$ 的每一位 $R_i$（其中 $i < n$），其计算基于以下布尔表达式：

1.和位 (Sum Bit, $R_i$)：三个输入位（$x_i$、$y_i$ 和进位 $c_i$）的异或 ($\oplus$) 结果：$R_i = x_i \oplus y_i \oplus c_i$

2.进位位 (Carry Bit, $c_{i+1}$)：下一位进位 $c_{i+1}$（即 $i+1$ 位运算的输入进位）可以通过公式递归计算：$c_{i+1} = x_i \cdot y_i \oplus c_i \cdot (x_i \oplus y_i)$ (其实是二阶基本对称函数$c_{i+1} = \sigma_2(x_i, y_i, c_i)$)，其中最低位 $c_0$ 被定义为 0。

至于减法，其实就是$X - Y = X + (-Y) = X + \neg Y + 1$，乘法也是加法和移位结合，于是MBA似乎可以转换为纯布尔表达式了，化简似乎也有了理论支持，这就是Arybo⁶干的事，它先用全加器做转换，然后使用petanque将布尔表达式转换为ANF形式，由于任何等价的表达式都具有唯一的ANF表示，所以可以直接做等价性判断，同时可以应用多种规则做规范化(化简)，规范化后它依然是位级布尔表示，我们阅读起来依然困难，还好Arybo支持在规范化后再反过来恢复(Identification出字级形式，此时可能仍然是MBA但是更简单了，可见⁷的使用样例，当然它的缺陷很明显，那就是位爆炸，像高位的进位依赖所有低位的结果，乘法也会极具膨胀，随着位数增加它的性能会急速下降。

基于代数

上面提到了 $BA[n]$ 定义的$n$是任意位都成立，其实zhou等人只证明了1比特转n比特都成立并用来构造恒等式，liu等人⁸证明了反过来也成立，即如果一个 MBA 恒等式在 $n$-bit 整数空间中成立，那么它必然在 1 比特空间中也成立，利用此性质可以将 $n$-bit 的混淆 MBA 表达式 $E_n$ 转换到 1-bit 空间中的 $E_1$，然后作者针对降维后的表达式提出了一种递归规约的算法，他们通过构建真值表发现，所有双变量（2 个变量）的 1-bit 布尔表达式（共 16 种情况）都可以表示为 $x, y, x \wedge y$ 和一个常数项的线性组合形式，即$c_1x + c_2y + c_3(x \wedge y) - c_4$，其中$x \wedge y$在此处可看作是乘法，其原始表达式关系和转换后的线性组合的常量表如下：

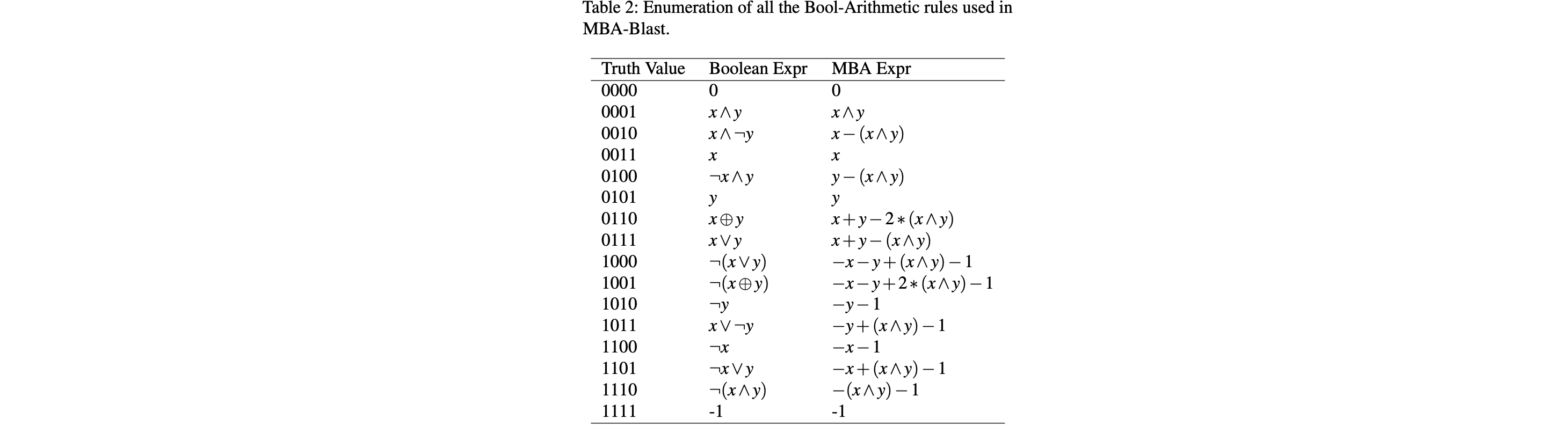
其实这和Arybo有点类似了，此处将MBA转换为了纯算术运算，递归的实施该过程就能将所有的表达式转换，之后再利用算术运算的规则(如交换律、结合律等)就能将其化简，化简后的结果又可直接扩展回$n$位。这就是MBA-Blast，后来又有了MBA-Solver⁹进一步优化性能，它们在线性MBA上能取得较好的结果。

Reichenwallner等人¹¹觉得这种方法还可以化简，于是提出了线性MBA解混淆器的终极版SiMBA，它建立了 $n$ 位空间中两个线性 MBA 表达式等价性的判断标准：

设 $e$ 和 $f$ 是字长为 $n$ 的线性 MBA 表达式， $t$ 是它们的最大变量数。那么 $e \equiv f$ 当且仅当 $e(b_i) = f(b_i)$ 对所有 $B^t$ 中的 $2^t$ 种可能的变量取值组合 $b_i$ 都成立。

这里的关键点是，对于线性 MBA 表达式，我们无需测试所有的 $2^n \times 2^n \times \dots$ 种可能的 $n$ 位输入值组合（如果变量多或$n$ 很大这根本不可能算出来），只需测试所有变量取 $0$ 或 $1$ 的 $2^t$ 种 $n$ 位输入组合，如果在这 $2^t$ 个测试点上两个表达式的值都相等，那么它们在整个 $n$ 位空间上就是等价的。(注：有个容易迷惑的点，我们的输入变量还是$n$ 位，但是它的值只取数字 $0$ 或 $1$，比如32位的变量取$1$为$0x00000001$ )

通过使用 $n$ 位值的输入组合 $b_i$ 来评估表达式 $e(b_i)$，可以直接得到 $n$ 位的结果，从而避免了将线性 MBA 分解为其项和因子，极大地简化了输入结构的要求，具体来说，SiMBA 算法通常包含三个步骤：

1.计算签名向量 $F$：通过对输入 MBA 表达式 $e$ 评估所有 $2^t$ 种变量的零和一组合来获得签名向量 $F$。

2.寻找线性组合：基于 $F$ 和定理 2，将输入 MBA 转换成基布尔表达式的线性组合。这种组合是有效的解决方案，但不一定是最佳的。

3.寻找更简单的解：如果结果涉及的变量少于三个，算法会尝试通过查找表进行多种优化尝试，以找到更简洁的表达式。例如，它能识别常量表达式、单个位表达式、否定表达式或更简单的线性组合。

虽然这篇论文里简单的提了下怎么简化多项式型MBA，但更进一步的工作还是在同作者的提出的GAMBA¹⁴上，它在SiMBA基础上做出了很多优化，但是主要是解决非线性MBA化简，它主要通过因式分解和非线性子表达式替换来处理非线性部分，之后识别线性子表达式用SiMBA取化简。

B3taMa0's Field

混合布尔算术MBA

定义与应用

定义

化简挑战

用途

分类

线性MBA(linear MBA)

多项式型MBA(polynomial MBA)

非多项式型MBA(not polynomial MBA)

构造

基于匹配与重写

基于零函数和置换多项式的构造

置换多项式构造

初代目

进化版

零函数与零理想

零函数恒等式

零理想

攻击

基于规则匹配

基于位爆炸(Bit-blasting)

基于代数

基于合成

基于机器学习

参考

定义与应用

定义

化简挑战

用途

分类

线性MBA(linear MBA)

多项式型MBA(polynomial MBA)

非多项式型MBA(not polynomial MBA)

构造

基于匹配与重写

基于零函数和置换多项式的构造

置换多项式构造

初代目

进化版

零函数与零理想

零函数恒等式

零理想

攻击

基于规则匹配

基于位爆炸(Bit-blasting)

基于代数

基于合成

基于机器学习

参考

social